
¿Por qué es importante la significancia estadística?
Descubre por qué la significancia estadística es importante en el análisis de datos, la investigación y la toma de decisiones empresariales. Aprende sobre valor...
Aprenda cómo la significancia estadística determina si los resultados son reales o producto del azar. Comprenda los valores p, las pruebas de hipótesis y las aplicaciones prácticas para su negocio en 2025.
La significancia estadística se utiliza para determinar si un resultado es producto del azar o causado por algún factor de interés. Si es estadísticamente significativo, es poco probable que haya ocurrido por casualidad.
La significancia estadística es un concepto fundamental en el análisis de datos que le ayuda a distinguir entre efectos genuinos y fluctuaciones aleatorias en sus datos. Cuando realiza experimentos, encuestas o analiza métricas empresariales, necesita un método fiable para determinar si los patrones que observa son reales o simplemente el resultado del azar. La significancia estadística proporciona este marco crítico utilizando principios matemáticos para evaluar la probabilidad de que los resultados observados ocurran si realmente no hubiera ningún efecto o diferencia entre los grupos que está comparando.
El concepto surgió del trabajo del estadístico Ronald Fisher a principios del siglo XX y se ha convertido en la piedra angular de las pruebas de hipótesis en prácticamente todos los campos que dependen del análisis de datos. Desde la investigación farmacéutica validando nuevos tratamientos hasta empresas de comercio electrónico que optimizan las tasas de conversión, la significancia estadística sirve como guardián entre los conocimientos accionables y las conclusiones engañosas. Entender cómo funciona la significancia estadística le permite tomar decisiones informadas respaldadas por evidencia sólida, en lugar de intuición o coincidencia.
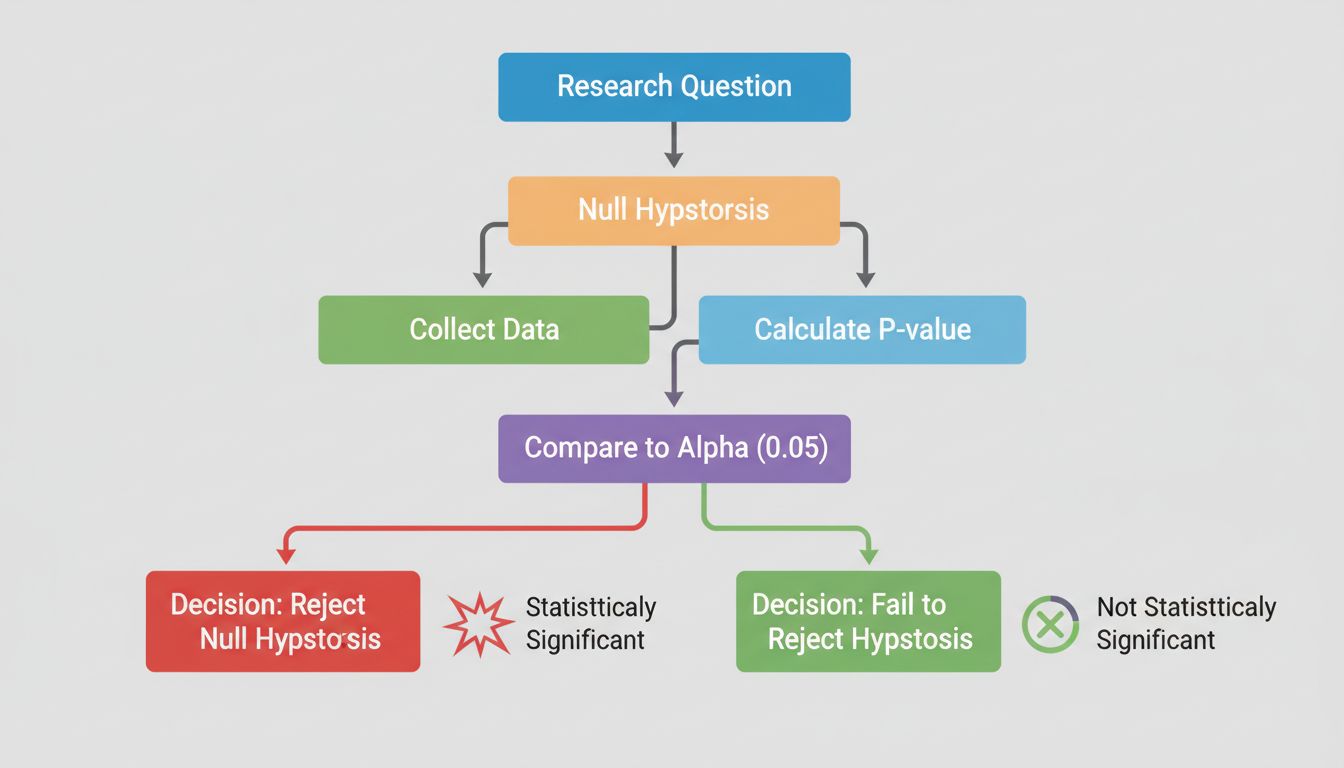
En el corazón de la significancia estadística se encuentra la prueba de hipótesis, una metodología estructurada para evaluar afirmaciones sobre sus datos. El proceso comienza formulando dos hipótesis opuestas: la hipótesis nula y la hipótesis alternativa. La hipótesis nula asume que no hay un efecto real ni diferencia entre los grupos que está estudiando; esencialmente, representa el statu quo o la suposición de que cualquier diferencia observada se debe puramente al azar. Por el contrario, la hipótesis alternativa propone que sí existe un efecto o diferencia real.
Considere un ejemplo práctico: está probando si una nueva campaña de marketing de afiliados genera tasas de conversión más altas que su enfoque actual. Su hipótesis nula sería que ambas campañas producen tasas de conversión idénticas, mientras que su hipótesis alternativa afirmaría que la nueva campaña tiene un rendimiento diferente. La prueba estadística evalúa cuál de las hipótesis es mejor respaldada por los datos. Este marco evita que los investigadores y analistas seleccionen únicamente los resultados que confirman sus expectativas; en cambio, les exige demostrar que sus hallazgos son poco probables de haber ocurrido por azar.
La belleza de la prueba de hipótesis es su objetividad. En lugar de basarse en juicios subjetivos, se emplean cálculos matemáticos para determinar si los datos proporcionan suficiente evidencia para rechazar la hipótesis nula. Si la evidencia es suficientemente fuerte, puede afirmar con confianza que el efecto observado es estadísticamente significativo, es decir, es poco probable que sea una casualidad.
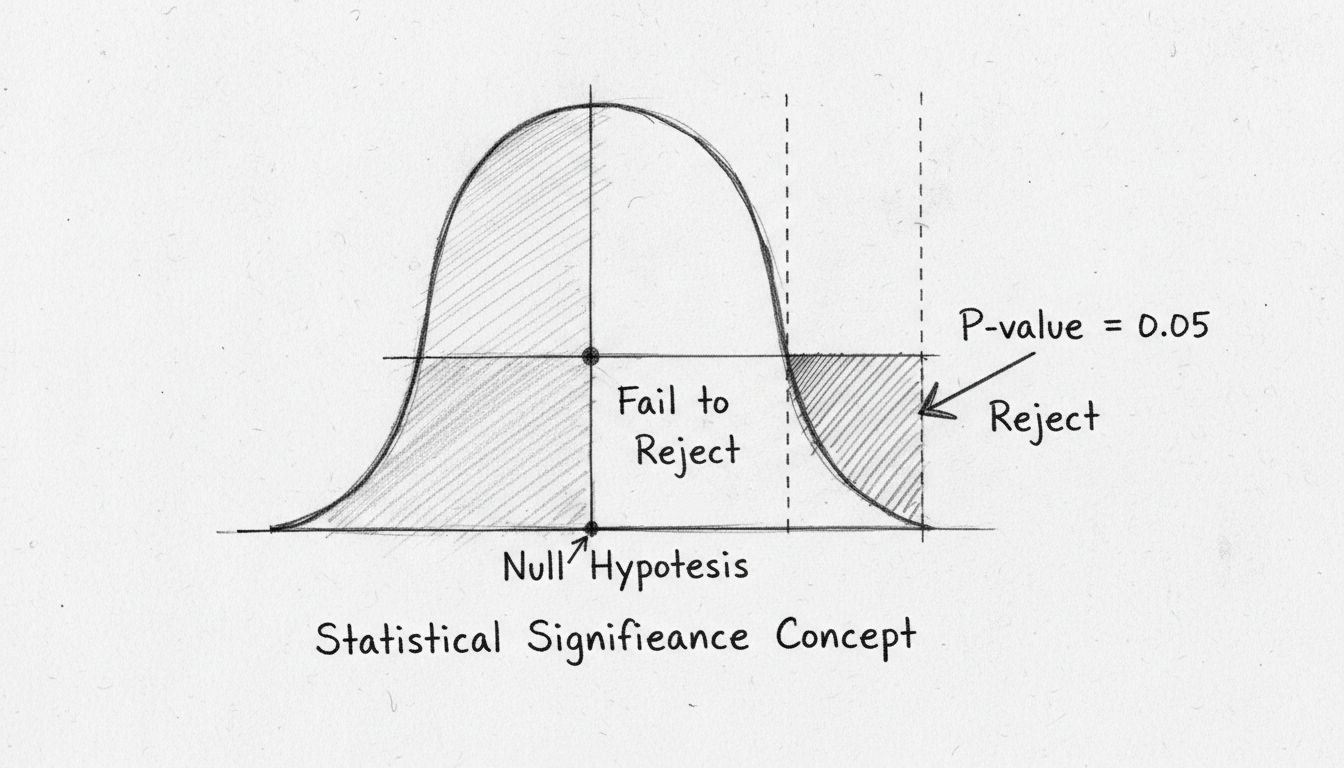
El valor p es quizás la métrica más utilizada en las pruebas de significancia estadística, aunque a menudo se malinterpreta. El valor p representa la probabilidad de observar sus resultados (o resultados aún más extremos) si la hipótesis nula fuera realmente cierta. En otras palabras, responde a la pregunta: “¿Qué tan probable es que vea estos datos si realmente no hubiera un efecto?” Un valor p pequeño indica que los resultados observados serían muy improbables bajo la hipótesis nula, sugiriendo que probablemente sea falsa y que su efecto es real.
El umbral convencional para la significancia estadística es un valor p de 0.05 o menos, lo que equivale a un 5% de probabilidad de que los resultados hayan ocurrido por azar. Esto significa que está dispuesto a aceptar un 5% de riesgo de rechazar incorrectamente la hipótesis nula cuando en realidad es cierta (lo que se denomina error de Tipo I). Sin embargo, este umbral es algo arbitrario y varía según el campo y el contexto. En la investigación médica, donde las consecuencias de los falsos positivos pueden ser graves, los investigadores suelen usar un umbral más estricto de 0.01 (1%). Por el contrario, en investigaciones exploratorias o pruebas tempranas, puede aceptarse un umbral de 0.10 (10%).
| Rango de valor p | Interpretación | Acción típica |
|---|---|---|
| p < 0.01 | Altamente significativo | Fuerte evidencia contra la hipótesis nula |
| 0.01 ≤ p < 0.05 | Significativo | Evidencia moderada contra la hipótesis nula |
| 0.05 ≤ p < 0.10 | Marginalmente significativo | Débil evidencia contra la hipótesis nula |
| p ≥ 0.10 | No significativo | Evidencia insuficiente para rechazar la hipótesis nula |
Es crucial entender lo que un valor p no le indica. Un valor p de 0.03 no significa que hay un 97% de probabilidad de que su hipótesis sea cierta. Tampoco mide el tamaño o la importancia práctica de su efecto. Un resultado estadísticamente significativo puede representar un efecto trivialmente pequeño que tiene poco impacto en el mundo real. Esta distinción entre significancia estadística y significancia práctica es una de las fuentes más comunes de confusión en el análisis de datos.
Mientras que los valores p le indican si existe un efecto, los intervalos de confianza proporcionan información crucial sobre la magnitud y precisión de ese efecto. Un intervalo de confianza es un rango de valores que probablemente contiene el verdadero tamaño del efecto, calculado con un nivel de confianza especificado (típicamente 95%). Si está probando si una nueva funcionalidad del programa de afiliados incrementa las comisiones, un intervalo de confianza del 95% podría indicar que el verdadero aumento se encuentra entre el 2% y el 8%, con un 95% de confianza de que el valor real está dentro de ese rango.
Los intervalos de confianza ofrecen varias ventajas sobre los valores p por sí solos. Primero, comunican tanto la dirección como la magnitud de un efecto, dándole una visión más completa de sus resultados. En segundo lugar, le ayudan a evaluar la significancia práctica: incluso si un efecto es estadísticamente significativo, si el intervalo de confianza muestra que el efecto es insignificante, puede que no merezca su implementación. Tercero, intervalos de confianza estrechos indican estimaciones precisas, mientras que intervalos amplios sugieren mayor incertidumbre en sus hallazgos.
El tamaño del efecto mide la fuerza de la relación entre variables o la magnitud de la diferencia entre grupos. Medidas comunes de tamaño del efecto incluyen d de Cohen (para comparar medias), coeficientes de correlación y razones de momios. Un efecto puede ser estadísticamente significativo pero tener un tamaño de efecto pequeño, lo que significa que el impacto práctico es mínimo. Por el contrario, un tamaño de efecto grande puede no alcanzar significancia estadística si su muestra es demasiado pequeña. Los analistas profesionales siempre reportan el tamaño del efecto junto con los valores p para proporcionar un panorama completo de sus hallazgos.
El tamaño de la muestra cumple un papel crítico en la determinación de la significancia estadística. Muestras más grandes proporcionan más información sobre su población y reducen el impacto de la variación aleatoria, facilitando la detección de efectos reales. Por el contrario, las muestras pequeñas son más susceptibles a fluctuaciones aleatorias, lo que puede llevar tanto a falsos positivos (detectar un efecto que no existe) como a falsos negativos (no detectar un efecto que sí existe).
La relación entre el tamaño de la muestra y el poder estadístico es fundamental en el diseño de la investigación. El poder estadístico es la probabilidad de rechazar correctamente la hipótesis nula cuando en realidad es falsa; esencialmente, su capacidad para detectar un efecto real. La mayoría de los investigadores buscan un poder de 0.80 (80%), lo que significa que aceptan un 20% de probabilidad de no detectar un efecto real. Para lograr este nivel de poder, necesita un tamaño de muestra suficientemente grande, que depende del tamaño del efecto esperado, el nivel de significancia elegido y el tipo de prueba estadística utilizada.
Antes de realizar cualquier estudio o experimento, los investigadores deben llevar a cabo un análisis de poder para determinar el tamaño de muestra requerido. Esto previene el desperdicio de recursos en estudios demasiado pequeños para detectar efectos significativos, y evita también estudios innecesariamente grandes que consumen tiempo y dinero en exceso. En el contexto del marketing de afiliados, esto significa determinar cuántas conversiones o clics necesita observar antes de poder concluir con confianza que un cambio en la campaña tiene un impacto real.
Diferentes preguntas de investigación y tipos de datos requieren distintas pruebas estadísticas. La elección de la prueba depende de factores como el número de grupos a comparar, si los datos tienen distribución normal, si las muestras son independientes o apareadas, y el tipo de variable de resultado (continua, categórica, etc.).
La prueba t de Student compara las medias de dos grupos y es una de las pruebas más utilizadas. Es apropiada cuando se tienen datos continuos (como montos de ingresos) y se desea saber si dos grupos difieren significativamente. La prueba tiene en cuenta la variabilidad dentro de cada grupo y los tamaños de muestra, produciendo un estadístico t que se compara con un valor crítico para determinar la significancia.
La prueba de chi-cuadrado se utiliza para datos categóricos para determinar si las frecuencias observadas difieren significativamente de las frecuencias esperadas. Si está analizando si el canal de afiliados (correo electrónico, redes sociales, anuncios de display) afecta las tasas de conversión, una prueba de chi-cuadrado sería apropiada.
El ANOVA (análisis de varianza) extiende la prueba t para comparar medias entre tres o más grupos simultáneamente. Esto previene el problema de comparaciones múltiples, donde realizar muchas pruebas separadas aumenta la probabilidad de falsos positivos.
Las pruebas U de Mann-Whitney y rango-suma de Wilcoxon son alternativas no paramétricas que se utilizan cuando los datos no cumplen los supuestos de las pruebas paramétricas, como cuando los datos no tienen distribución normal.
En el mundo empresarial, la significancia estadística guía la toma de decisiones críticas en numerosas funciones. Los equipos de marketing utilizan pruebas A/B con significancia estadística para determinar si los cambios en el sitio web, los asuntos de correos o los creativos publicitarios realmente mejoran los indicadores de rendimiento. En lugar de confiar en corazonadas o observaciones de muestras pequeñas, las empresas basadas en datos establecen umbrales de significancia antes de ejecutar pruebas, asegurándose de que las decisiones se fundamenten en evidencia fiable.
En el marketing de afiliados específicamente, la significancia estadística le ayuda a identificar qué afiliados, campañas y estrategias promocionales realmente generan ingresos, frente a aquellas que parecen exitosas solo por variaciones aleatorias. Cuando evalúa si una nueva estructura de comisiones aumenta el rendimiento de los afiliados, las pruebas estadísticas le evitan realizar cambios costosos basados en fluctuaciones a corto plazo. La plataforma avanzada de análisis de PostAffiliatePro le permite rastrear métricas de afiliados con el rigor estadístico necesario para tomar decisiones de optimización con confianza.
En la investigación farmacéutica y médica, la significancia estadística determina si los nuevos tratamientos son lo suficientemente efectivos para justificar su aprobación y uso. Los ensayos clínicos deben demostrar que los beneficios de un fármaco son estadísticamente significativos antes de que pueda recetarse a los pacientes. Las apuestas son altas, por lo que la investigación médica suele usar niveles de significancia más estrictos que otros campos.
Uno de los conceptos erróneos más extendidos es que la significancia estadística prueba la causalidad. Una correlación estadísticamente significativa entre dos variables no significa que una cause la otra. El ejemplo clásico es la fuerte correlación entre estrenos de películas de Nicolas Cage y ahogamientos en piscinas; claramente, uno no causa el otro. La significancia estadística solo indica que una relación es poco probable que se deba al azar; establecer la causalidad requiere evidencia adicional, como un mecanismo lógico, orden temporal y experimentos controlados.
Otro error común es el p-hacking o minería de datos, donde los investigadores realizan numerosas pruebas estadísticas sobre el mismo conjunto de datos hasta encontrar resultados significativos. Esta práctica aumenta artificialmente la probabilidad de falsos positivos porque, con suficientes pruebas, inevitablemente se encuentra algo significativo por puro azar. Si realiza 20 pruebas independientes con un nivel de significancia de 0.05, esperaría encontrar aproximadamente un falso positivo solo por azar. Los investigadores responsables preespecifican sus hipótesis y pruebas estadísticas antes de analizar los datos, evitando este problema.
Malinterpretar los resultados no significativos es otra trampa. Un resultado no significativo no prueba que no exista un efecto; simplemente significa que no hay suficiente evidencia para rechazar la hipótesis nula. Esto puede deberse a un tamaño de muestra insuficiente, alta variabilidad en los datos o a la ausencia genuina de un efecto. La ausencia de evidencia no es evidencia de ausencia.
El campo de la estadística sigue evolucionando, con un reconocimiento creciente de las limitaciones de los enfoques tradicionales basados en valores p. Muchos estadísticos ahora abogan por un enfoque más matizado que combine valores p con tamaños de efecto, intervalos de confianza y métodos bayesianos. La estadística bayesiana, que incorpora conocimientos previos y actualiza creencias en función de los datos observados, ofrece un marco alternativo que algunos investigadores consideran más intuitivo y flexible que los enfoques frecuentistas.
Las pruebas secuenciales y los diseños adaptativos han cobrado relevancia, permitiendo a los investigadores monitorear resultados a medida que se acumulan los datos y tomar decisiones sobre continuar, modificar o detener estudios basándose en análisis intermedios. Este enfoque es especialmente valioso en contextos empresariales donde las decisiones deben tomarse rápidamente. Herramientas como Stats Engine de Statsig implementan pruebas secuenciales con control de la tasa de descubrimientos falsos, permitiendo una toma de decisiones más rápida y precisa durante los experimentos.
La crisis de replicación en la ciencia también ha destacado la importancia de comprender correctamente la significancia estadística. Muchos hallazgos publicados no se replican, en parte porque los investigadores y las revistas se han enfocado excesivamente en lograr significancia estadística, ignorando el tamaño del efecto y la significancia práctica. En el futuro, el énfasis estará en la transparencia, la preinscripción de estudios y la publicación de todos los resultados sin importar su significancia.
Para utilizar la significancia estadística de manera efectiva, establezca su nivel de significancia y los requisitos de tamaño de muestra antes de realizar su análisis. Esto evita la tentación de ajustar los umbrales después de ver los resultados. Siempre reporte los tamaños de efecto y los intervalos de confianza junto con los valores p para proporcionar un panorama completo de sus hallazgos. Considere la significancia práctica de sus resultados: un efecto estadísticamente significativo podría ser demasiado pequeño para ser relevante en aplicaciones del mundo real.
Sea transparente con su metodología, incluyendo cómo manejó los datos faltantes, valores atípicos y comparaciones múltiples. Si realizó múltiples pruebas, aplique correcciones apropiadas como la corrección de Bonferroni para mantener su nivel de significancia general. Documente su proceso de análisis y esté dispuesto a compartir sus datos y código con otros para verificación y replicación.
Por último, recuerde que la significancia estadística es una herramienta, no un destino. Le ayuda a tomar mejores decisiones reduciendo la influencia del azar, pero debe combinarse con experiencia en el área, consideraciones prácticas y juicio empresarial. En el marketing de afiliados, la significancia estadística le ayuda a identificar cuáles estrategias realmente mejoran el rendimiento, pero también debe considerar factores como costos de implementación, satisfacción de los afiliados y sostenibilidad a largo plazo al tomar decisiones estratégicas.
Las herramientas avanzadas de análisis e informes de PostAffiliatePro le ayudan a rastrear el rendimiento de los afiliados con rigor estadístico. Comprenda qué campañas realmente generan resultados y optimice su programa de afiliados basándose en conocimientos fiables de los datos.

Descubre por qué la significancia estadística es importante en el análisis de datos, la investigación y la toma de decisiones empresariales. Aprende sobre valor...
La significancia estadística expresa la fiabilidad de los datos medidos, ayudando a las empresas a distinguir los efectos reales del azar y a tomar decisiones i...
Domina la significancia estadística en pruebas A/B para campañas de afiliados de apuestas.
Consentimiento de Cookies
Usamos cookies para mejorar tu experiencia de navegación y analizar nuestro tráfico. See our privacy policy.